Jeżeli potrzebują Państwo szybko wykonać pomiary obrabianego elementu, nie inwestując przy tym w instrumenty kontrolne lub jeżeli wydajność pomiarowa w Państwa zakładzie jest czasami niewystarczająca to zapraszamy do współpracy!
|
Zakres usług pomiarowych obejmuje:
- kompleksowe pomiary elementów o skomplikowanych kształtach oraz przyrządów technologicznych
- pomiary odchyłek położenia i kształtu
- pomiary serii z wykorzystaniem programów pomiarowych
- kontrola wymiarów oraz odchyłek położenia i kształtu detalu na etapie wykonywania prototypów jak również produkcji seryjnej
- przygotowanie profesjonalnych raportów pomiarowych z uwzględnieniem wymagań klienta
Korzyści zastosowania pomiarów współrzędnościową maszyną pomiarową
- wykonanie pomiarów z bardzo dużą dokładnością
- zdecydowane skrócenie czasu pomiaru detalu
- wyeliminowanie stosowania wielu podstawowych przyrządów pomiarowych dla wykonania pomiaru
- dostęp do profesjonalnie opracowanych raportów pomiarowych wymaganych w przemyśle maszynowym, samochodowym oraz lotniczym
Jak wyceniamy usługę pomiaru:
W przypadku pomiaru współrzędnościową maszyną pomiarową koszt oraz czas wykonania pomiaru uzależniony jest od ilości wymaganych punktów pomiarowych, stopnia skomplikowania kształtu detalu oraz ilości mierzonych detali. W celu przygotowania wyceny prosimy o przesłanie rysunku detalu oraz jego modelu CAD z określeniem zakresu pomiarów.
Zapytania prosimy przesyłać na adres: office@igel-cmm.com
|
|
 |
NASZE REALIZACJE:
| |
 |
|
Właściwie wyprodukowany wyrób musi mieć odpowiednie cechy przewidziane w warunkach technicznych, takie jak: twardość, wytrzymałość, struktura, skład chemiczny, itp. Jednym z najważniejszych warunków decydujących o wartości użytkowej produktu jest nadanie mu właściwej postaci geometrycznej w procesie produkcyjnym, w którym funkcję kontrolną pełnią pomiary długości i kąta. Doskonalenie sposobów pomiaru i przyrządów pomiarowych ma zatem duży wpływ na poprawę jakości produkcji, warunkuje postęp techniczny, zwłaszcza w tych dziedzinach, w których są stawiane coraz większe wymagania dokładnościowe, a także przyczynia się do poprawy niezawodności wyrobów i wydajności pracy.
Ważną rolę w technice odgrywa metrologia wielkości geometrycznych, zajmująca się pomiarami długości i kąta w celu określenia geometrycznej postaci części maszyn i urządzeń technicznych, w szczególności związanych z przemysłem motoryzacyjnym.
Metrologia jest dziedziną obejmującą:
- pomiary wymiarów opisujących postać geometryczną mierzonego elementu lub zespołu,
- pomiary odstępstw od teoretycznego kształtu powierzchni i linii oraz odstępstw od przyjętego wzajemnego położenia wyodrębnionych linii i powierzchni (odchyłki geometryczne)
- pomiary ilościowe struktury geometrycznej powierzchni (chropowatość i falistość powierzchni)
|
I. Istota pomiarów współrzędnościowych
Współrzędnościowa technika pomiarowa charakteryzuje się odmienną od klasycznej metrologii strategią pomiarową. Opiera się na przetwarzanych komputerowo informacjach pomiarowych w postaci dyskretnej i umożliwia wyznaczenie wymiarów przestrzennie ukształtowanych części maszyn, ze stosunkowo wysoką dokładnością. Technika pomiarowa charakteryzuje się procedurami pomiarowymi opartymi na wartościach współrzędnych punktów. Punkty te są lokalizowane podczas procesu pomiarowego i są podstawą do wyznaczenia wszystkich geometrycznych figur, z których składa się element mierzony.
We współrzędnościowej technice pomiarowej podstawą jest maszyna (Coordinate Measuring Machine - CMM), której zespoły ruchome mogą się przemieszczać w trzech wzajemnie prostopadłych kierunkach. Kierunki te oznaczone są jako osie X,Y,Z maszyny i przedstawiają przestrzenny okład współrzędnych. Przesunięcia wzdłuż osi są wskazywane przez wzorce długości i przesyłane do pamięci komputerowych i elektronicznych zespołów sterujących. W odróżnieniu od konwencjonalnych metod pomiaru, pomiar może odbywać się w dowolnym położeniu przedmiotu. Korekta nierównoległości osi pomiarowej przyrządu z osią mierzonego wymiaru jest przeprowadzana komputerowo, przy czym relacje między kątami pochylenia osi są wyznaczone uprzednio w procesie pomiarowym.
|
| |
 |
|
II. Kalibracja głowicy pomiarowej
By móc przystąpić do pomiaru bardzo ważnym elementem jest kalibracja głowicy pomiarowej. Istota wzorcowania polega na sprowadzeniu poszczególnych końcówek do jednego wyimaginowanego, punktu przestrzeni, którego dokładne położenie obliczone jest rachunkowo. Zwykle jest nim oś końcówki przebiegającej wzdłuż osi głowicy. Sam proces kalibracji przeprowadza się, dokonując pomiary kuli wzorcowej o znanej średnicy.
|
| |
Mając dane o średnicy kuli wzorcowej, komputer maszyny jest w stanie obliczyć wszystkie potrzebne informacje, niezbędne do dokonania bezbłędnych pomiarów. Proces kalibracji należy wykonać jako pierwszy w procesie pomiaru, zawsze po wyposażeniu głowicy w zestawy trzpieni i końcówek pomiarowych.
Wektor korekcji promienia końcówki pomiarowej jest stosowany do przekształcenia punktu pomiarowego zaobserwowanego w punkt pomiarowy skorygowany i obejmuje zwykle fizyczny wymiar końcówki trzpienia pomiarowego (np. promień) i korekcję błędu systematycznego zespołu głowicy pomiarowej. W praktyce do ustalenia długości wektora korekcji promienia zwykle stosuje się przybliżoną wartość promienia końcówki, a do wyznaczenia kierunku wykorzystuje się przybliżenie normalnej do powierzchni.
Średnica końcówki uwzględnia czynniki wynikające z procesu korekcji takie jak ugięcie trzpienia pomiarowego i jest zwykle nazwana efektywną średnicą końcówki trzpienia pomiarowego. |
|

|
III. Układ współrzędnych maszyny i przedmiotu
W przypadku konwencjonalnych metod pomiarowych, by przeprowadzić pomiary przedmiotu należy go odpowiednio ustawić i zamocować, np. równolegle do kierunku pomiaru lub w osi mierzonego elementu. Powoduje to wzrost pracochłonności, komplikując i wydłużając czas pomiaru. Wielką zaletą pomiarów na maszynach współrzędnościowych jest to, że można element ustawić prawie dowolnie, zaś dopasowanie przedmiotu do układu współrzędnych odbywa się rachunkowo. Chociaż maszyna dysponuje własnym układem współrzędnych to można przez ustalenie położenia przedmiotu w przestrzeni zdefiniować (jeszcze przed rozpoczęciem pomiarów) nowy układ obowiązujący dla danego elementu. |

|
|
Powstaje pytanie zatem w jaki sposób sensownie zdefiniować i wymierzyć układ odniesienia?
W przygotowaniu procedury pomiarowej jest to najtrudniejsza część zadania i wymaga od operatora pewnego doświadczenia. Prawidłowo zorientowany detal to taki, któremu odebrano wszystkie 6 stopni swobody, a więc określono poziom, obrót oraz początek układu współrzędnych.
- Poziom - W tym kroku wskazujemy maszynie położenie części w osi Z (wysokość). W większości przypadków będzie to płaszczyzna równoległa do płaszczyzny XY maszyny. W zdecydowanej większości przypadków elementem określającym płaszczyznę bazową XY będzie zmierzona płaszczyzna.
- Obrót - Po określeniu płaszczyzny nasza część nie może być już poruszana w górę i w dół, wciąż jednak możemy dowolnie nią obracać i przesuwać. Aby ograniczyć te możliwości, określimy wyrównanie detalu do jednej z osi – X lub Y. Dokonamy tego mierząc np. jedną z powierzchni bocznych jako linię lub płaszczyznę.
- Początek układu (punkt 0,0,0) - Nasza część leży w pewnej płaszczyźnie i jest równoległa do jednej z osi – nie możemy więc już ani jej podnosić, ani obracać. Poprzez wyrównanie do osi X lub Y odebraliśmy jej kolejne stopnie swobody. Należy wskazać teraz element, który określi nam początek układu. Może być to zarówno środek okręgu czy sfery, jak i punkt utworzony z przecięcia dwóch prostych, czy też po prostu pojedynczy punkt
Powyższa metoda należy do powszechnie stosowanych strategii budowy układu współrzędnych i wpisuje się tzw. metodę 3-2-1, która określa schemat budowania układów w logicznej kolejności – najpierw 3 punkty na płaszczyźnie, następnie 2 punkty tworzące linię i wreszcie 1 punkt będący początkiem układu (PLP – płaszczyzna, linia, punkt). |
Czasami rysunek wykonawczy zawiera więcej niż jeden układ współrzędnych. Rysunki części mają często pojedyncze wymiary zdefiniowane we własnym układzie odniesienia. Także ten problem można różnorodnie rozwiązać, gdyż większość oprogramowań pozwala w dowolnym momencie zdefiniować nowy układ współrzędnych, tzw. układ podrzędny. Przy umiejętnym zaplanowaniu pomiarów możliwe jest otrzymanie takiego protokołu, w którym wszystkie wyniki można przetransformować w dowolny układ odniesienia.
IV. Geometryczne elementy bazowe
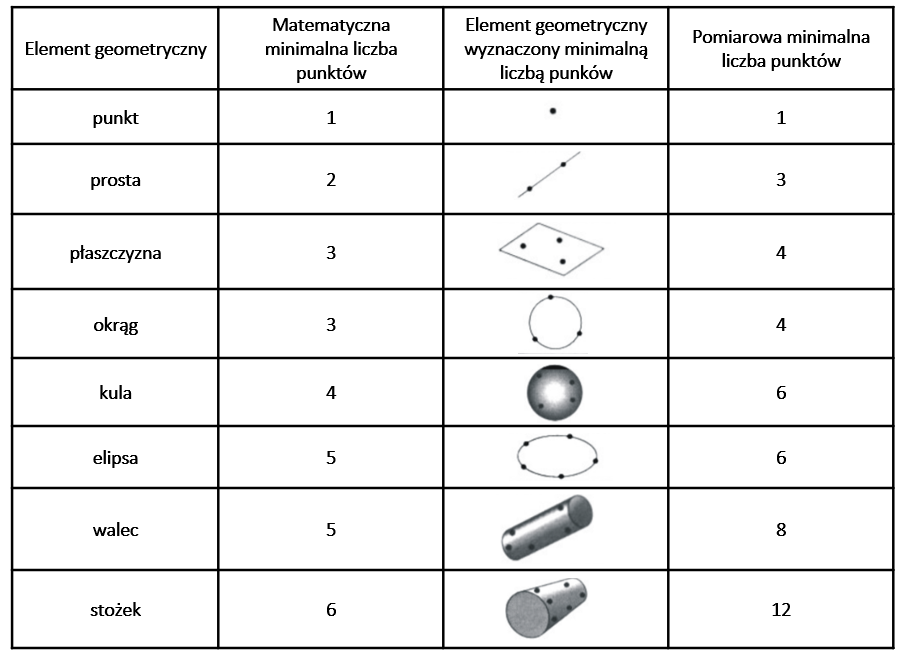
Powierzchnię każdego mierzonego przedmiotu można opisać za pomocą podstawowych elementów geometrycznych. Należą do nich: punkt, prosta, płaszczyzna, okrąg, kula, walec, stożek. Czasami dochodzą do tego figury dodatkowe, jak elipsa, pierścień, torus, itp. Zatem przez matematyczne wyznaczenie parametrów figur oraz brył geometrycznych można opisać położenie w przestrzeni pomiarowej maszyny, poszczególnych części mierzonego przedmiotu.
|
| |
 |
|
We współrzędnościowej technice pomiarowej do wyznaczenia każdego z wyżej wymienionych elementów przedmiotu wykorzystuje się współrzedne punktów należących fo danego elementu. Współrzędne te otrzymywane są bezpośrednio z pomiaru lub z wyniku obliczeń. Każdy z elementów geometrycznych ma dwie tzw. minimalne liczby punktów potrzebnych do jego zdefiniowania. Są to: matematyczna minimalna liczba punktów - wynika z liczby stopni swobody, jaką ma element oraz pomiarowa minimalna liczba punktów - jest tak dobrana, aby wpływ najmniejszej odchyłki kształtu na wynik był nieistotny.
V. Relacje między elementami geometrycznymi
Obliczenie podstawowych parametrów figur geometrycznych, wchodzących w skład mierzonego przedmiotu, jest w większości przypadków niewystarczające. Przy sprawdzeniu wymiarów danego przedmiotu potrzebne są informacje o wzajemnych odległościach, grubościach ścian, kątach pochylenia osi i płaszczyzn, rzutach i przekrojach, itp. - dlatego też każdy typowy program obliczeniowy, sprzężony z maszyną współrzędnościową, zawiera procedury obliczeniowe relacji między elementami geometrycznymi. Program obliczeniowy obejmuje dodatkowo pewne przekształcenia i konstrukcje potrzebne do wyznaczenia wymiarów, które nie mogą być zmierzone bezpośrednio. Są takie przekształcenia i konstrukcje jak:
|
- obliczenie elementów przecięcia,
- symetria i odbicie lustrzane względem osi i płaszczyzny,
- wykonywanie przekrojów przedmiotu mierzonego.
Programy do obsługi maszyn współrzędnościowych zawierają, oprócz wyżej wymienionych opcji, również procedury wyznaczania typowych odchyłek kształtu, takich jak np.: prostoliniowość, okrągłość, płaskość, walcowość itp. Ponadto program zazwyczaj daje możliwość wyznaczenia typowych odchyłek położenia i bicia, takich jak: równoległość, prostopadłość, tolerancja kąta, współśrodkowość, współosiowość, symetria, bicie wzdłużne, bicie poprzeczne. W odróżnieniu od procedur wyznaczania głównych figur geometrycznych, dokładność wyznaczania odchyłek kształtu i położenia zależy w dużym stopniu od liczby punktów pomiarowych. W tym przypadku minimalna liczba punktów jest niewystarczająca ( w praktyce wynosi ona kilkanaście, a nawet kilkaset).
Często zachodzi sytuacja, w której dany wymiar podany na rysunku wykonawczym przedmiotu nie może być zmierzony bezpośrednio. konieczne jest wtedy dokonanie pewnych przekształceń i konstrukcji, takich jak obliczenie elementów przecięcia, symetrii i odbić lustrzanych względem osi i płaszczyzn, rzutowanie, dokonywanie przekrojów przedmiotu mierzonego. Typowy program przystosowany do współpracy z maszyną współrzędnościową obejmuje przykładowo następujące konstrukcje:
- punkt symetrii dwóch punktów usytuowanych dowolnie w przestrzeni lub leżących na jednej z płaszczyzn układu współrzędnych
- okrąg zawierający środki trzech, lub więcej, innych okręgów
- linia prosta przechodząca przez środki dwóch, lub więcej, kul
- okrąg zawierający środki trzech, lub więcej, innych okręgów
- płaszczyzna symetrii dwóch płaszczyzn
- rzut punktu w przestrzeni na płaszczyznę lub prostą w przestrzeni
- rzut prostej w przestrzeni na dowolną płaszczyznę
- punkt przecięcia dwóch prostych leżących na tej samej płaszczyźnie
- punkt przecięcia prostej w przestrzeni z płaszczyzną lub kulą; krawędź przecięcia dwóch płaszczyzn
- środek i średnica okręgu jako wynik przecięcia kuli i płaszczyzny lub dwóch kul
|
|
 |
Oprócz wyżej wymienionych opcji programy do obsługi maszyn współrzędnościowych zawierają zazwyczaj procedury wyznaczania typowych odchyłek kształtu, jak np.: prostoliniowości, okrągłości, płaskości, walcowości itp. istnieje również możliwość wyznaczenia typowych odchyłek położenia i bicia, a mianowicie: równoległości, prostopadłości, tolerancji kąta, współśrodkowości, współosiowości, symetrii, bicia wzdłużnego i bicia poprzecznego.
|
| Źródło: Eugeniusz Ratajczyk, Współrzędnościowa technika pomiarowa, Oficyna Wydawnicza Politechniki Warszawskiej 2005. |
